Tài liệu đề cương ôn thi vào lớp 10 môn toán
Đề cương ôn thi vào 10 môn toán này là tài liệu mà mỗi học sinh cần có để giúp ôn thi môn toán vào lớp 10 hiệu quả nhất.
Đề cương này được soạn theo từng chuyên đề ôn thi cụ thể giúp học sinh dễ dàng hình dung được những vấn đề cần nắm trong việc ôn tập toán thi vào 10.
1. Các phép biến đổi về căn thức
Phần này được soạn chi tiết hơn và có nhiều bài tập điển hình để luyện tập, chúng tôi đã thể hiện ở bài viết: Chuyên đề Rút Gọn Biểu Thức toán lớp 9
Lý thuyết cần nắm

Các dạng bài tập cơ bản của chuyên đề các phép biến đổi căn thức
Dạng 1: Tính giá trị biểu thức
Phương pháp tính giá trị biểu thức:
Bước 1: Trục căn thức ở mẫu (nếu có)
Bước 2: Qui đồng mẫu thức (nếu có)
Bước 3: Đưa một biểu thức ra ngoài dấu căn
Bước 4: Rút gọn biểu thức
Bước 5: Tính số trị (nếu còn tham số)
Dạng 2: Rút gọn biểu thức
Phương pháp rút gọn biểu thức:
Bước 1: Tìm điều kiện xác định của biểu thức
Bước 2: Trục căn thức ở mẫu nếu có (nếu có)
Bước 3: Qui đồng mẫu thức (nếu có)
Bước 4: Đưa một biểu thức ra ngoài dấu căn
Bước 5: Rút gọn biểu thức
Dạng 3: Chứng minh đẳng thức
Phương pháp chứng minh đẳng thức:
Bước 1: Tìm điều kiện xác định của biểu thức
Bước 2: Biến đổi vế trái về vế phải hoặc vế phải về vế trái. Cũng có khi chúng ta phải biến đổi cả hai vế cùng về biểu thức trung gian
2. Phương trình bậc hai một ẩn
- Lý thuyết cần nắm
Dạng 1: Tìm điều kiện để phương trình bậc hai có nghiệm
Phương pháp:
Điều kiện để phương trình bậc hai có nghiệm là Denta = b2 – 4ac >= 0 hoặc c/a <= 0
Trong trường hợp cần chứng minh có ít nhất một trong hai phương trình ax2 + bx + c = 0 (có Denta 1), a’x2 + b’x + c = 0 (có Denta 2) có nghiệm người ta thường làm theo một trong hai cách sau:
Cách 1: Chứng minh Denta1 + Denta 2 >= 0
Cách 2: Chứng minh Denta1.Denta 2 <= 0
Dạng 2: Tìm hai số khi biết tổng và tích
Phương pháp:
Bước 1: Cho hai số x, y biết x + y = S; x.y = P thì x, y là hai nghiệm của phương trình bậc hai X2 – SX + P = 0
Bước 2: Giải phương trình X2 – SX + P = 0
Bước 3: Kết luận
3. Hệ phương trình
- Hệ phương trình bậc nhất hai ẩn số:
Cách 1: Sử dụng phương pháp cộng đại số:
– Nhân các vế của hai phương trình với số thích hợp (nếu cần) sao cho các hệ số của một ẩn nào đó trong hai phương trình của hệ bằng nhau hoặc đối nhau
– Sử dụng quy tắc cộng đại số để thực hiện phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn số)
– Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ phương trình đã cho
Cách 2: Sử dụng phương pháp thế
– Dùng quy tắc thế biến đổi hệ phương trình đã cho để được hệ phương trình mới, trong đó
có một phương trình một ẩn
– Giải phương trình một ẩn vừa có, rồi suy ra nghiệm của hệ đã cho
- Hệ phương trình đối xứng
a) Hệ đối xứng loại I: Nếu ta thay đổi vai trò của x, y thì từng phương trình không thay đổi
Phương pháp: Đưa về hệ phương trình theo hai biến mới là: S = x + y và P = xy với điều kiện S2 >= 4P
b) Hệ đối xứng loại II: Nếu ta thay đổi vai trò của x, y thì phương trình này chuyển thành phương trình kia
Phương pháp: Trừ hai phương trình với nhau để nhận được phương trình mới có dạng tích số. Chú ý nếu hệ phương trình có nghiệm (x0; x0) (tức là x = y). Nếu hệ phương trình có nghiệm (x, y) thì phương trình cũng có nghiệm (y, x)
4. Phương trình quy về phương trình bậc nhất (bậc hai)
1. Phương trình chứa ẩn ở mẫu số:
Phương pháp:
Bước 1: Đặt điều kiện để phương trình có nghĩa
Bước 2: Qui đồng mẫu số để đa về phương trình bậc nhất (bậc hai)
Bước 3: Giải phương trình bậc nhất (bậc hai) trên
Bước 4: So sánh với điều kiện và kết luận nghiệm
Ngoài ra còn có phương trình chứa dấu giá trị tuyệt đối.
5. Giải bài toán bằng cách lập phương trình, hệ phương trình
Phương pháp chung
– Chọn ẩn số và xác định điều kiện của ẩn số (đơn vị tính). Ẩn số thường là đại lượng chưa biết trong bài toán. Việc chọn một ẩn số hay hai ẩn số tuỳ thuộc vào số đại lượng chưa biết trong bài toán
– Biểu diễn mối tương quan giữa đại lượng đã biết và đại lượng chưa biết
– Lập phương trình (hay hệ phương trình)
– Giải phương trình (hay hệ phương trình)
– Nhận định kết quả và trả lời
Phần này pqt.edu.vn đã có bài viết riêng trình bày cụ thể hơn lý thuyết và các dạng toán thường gặp, xin xem thêm tại: Làm sao để giải bài toán bằng cách lập phương trình
6. Hệ thức lượng trong tam giác vuông

7. Đường tròn
- Kiến thức lý thuyết về đường tròn lớp 9
Xem thêm: Cách chứng minh tứ giác nội tiếp đường tròn đạt điểm tối đa
a) Sự xác định đường tròn. Tính chất đối xứng của đường tròn
– Đường tròn tâm O bán kính R (với R > 0) là hình gồm các điểm cách đều điểm O một khoảng bằng R
– Tuỳ theo OM = R; OM < R; OM > R mà ta có điểm M nằm trên, nằm bên trong, nằm bên ngoài đường tròn
– Qua ba điểm không thẳng hàng, bao giờ cũng vẽ được một và chỉ một đường tròn
– Đường tròn có tâm đối xứng, đó là tâm đường tròn. Đường tròn có vô số trục đối xứng, đó là bất kì đường kính nào của nó
b) Đường kính và dây cung của đường tròn. Liên hệ giữa dây và khoảng cách từ tâm đến dây
– Trong một đường tròn, dây lớn nhất là đường kính
– Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy
– Đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy
– Trong một đường tròn: Hai dây bằng nhau khi và chỉ khi chúng cách đều tâm. Trong hai dây không bằng nhau, dây lớn hơn khi và chỉ khi nó gần tâm hơn
c) Vị trí tương đối của đường thẳng và đường tròn. Dấu hiệu nhận biết tiếp tuyến của đường tròn
Căn cứ vào số điểm chung 0, 1, 2 của đường thẳng và đường tròn mà ta định nghĩa các vị trí: đường thẳng và đường tròn không giao nhau; tiếp xúc nhau; cắt nhau. Ứng với mỗi vị trí trên, khoảng cách d từ tâm đường tròn đến đường thẳng và bán kính R của đường tròn có các liên hệ: d > R; d = R; d < R. Ta có các định lí
– Nếu một đường thẳng là tiếp tuyến của đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm
– Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn
d) Tính chất của hai tiếp tuyến cắt nhau:
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
– Điểm đó cách đều hai tiếp điểm
– Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến. Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm
e) Đường tròn nội tiếp tam giác, ngoại tiếp tam giác, bàng tiếp tam giác
– Đường tròn tiếp xúc với ba cạnh của một tam giác gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn. Tâm của đường tròn nội tiếp tam giác là giao điểm của các đường phân giác các góc trong tam giác
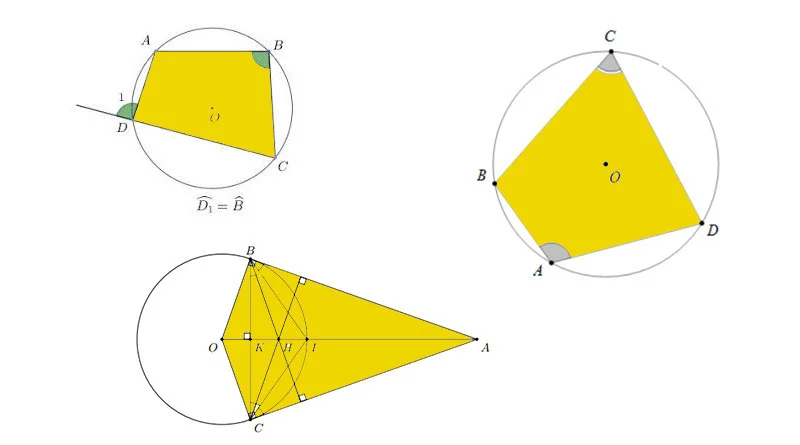
– Đường tròn đi qua ba đỉnh của một tam giác gọi là đường tròn ngoại tiếp tam giác, còn tam giác gọi là nội tiếp đường tròn. Tâm của đường tròn ngoại tiếp tam giác là giao điểm của các đường trung trực tam giác
– Đường tròn tiếp xúc với một cạnh của một tam giác và tiếp xúc với phần kéo dài của hai cạnh kia là đường tròn bàng tiếp tam giác. Tâm của mỗi đường tròn bàng tiếp tam giác là giao
điểm của hai đường phân giác của hai góc ngoài tam giác hoặc giao điểm của tia phân giác của một góc trong và một trong hai đường phân giác của góc ngoài không kề với nó
f) Vị trí tương đối của hai đường tròn
Căn cứ vào số điểm chung 0, 1, 2 của hai đường tròn mà ta định nghĩa các vị trí: Hai đường tròn không giao nhau, tiếp xúc nhau, cắt nhau
Do tính chất đối xứng của đường tròn, nếu hai đường tròn cắt nhau thì giao điểm đối xứng với nhau qua đường nối tâm, nếu hai đường tròn tiếp xúc nhau thì giao điểm nằm trên đường nối
tâm
g) Góc với đường tròn:
+ Góc ở tâm: Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm. Số đo cung nhỏ bằng số đo của góc ở tâm chắn cung đó. Số đo cung lớn bằng hiệu giữa 3600 và số đo cung nhỏ. Số đo của nửa đường tròn bằng 1800
+ Góc nội tiếp: Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa dây cung của đường tròn đó. Cung bên trong của góc gọi là cung bị chắn. Trong một đường tròn số đo của
góc nội tiếp bằng nữa số đo cung bị chắn
+ Góc tạo bởi giữa tiếp tuyến và dây cung: Cho đường tròn (O), A là tiếp điểm, xAy là tiếp tuyến của (O) tại A, AB là một dây cung. Góc tạo bởi tia Ax (hoặc tia Ay) với dây AB được gọi
là góc tạo bởi tiếp tuyến và dây cung. Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nữa số đo cung bị chắn
+ Góc có đỉnh ở bên trong đường tròn: Mỗi góc có đỉnh ở bên trong đường tròn chắn hai cung: một cung nằm bên trong góc và cung kia nằm bên trong góc đối đỉnh của cung đó. Số đo có
đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn
+ Góc có đỉnh ở bên ngoài đường tròn: Số đo góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu hai cung bị chắn
Chú ý: Trong một đường tròn
– Các góc nội tiếp bằng nhau chắn các cung bằng nhau
– Các góc nội tiếp cùng chắn một cung thì bằng nhau
– Các góc nội tiếp chắn các cung bằng nhau thì bằng nhau
– Góc nội tiếp nhỏ hơn hoặc bằng 900 có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
– Góc nội tiếp chắn nửa đường tròn là góc vuông và ngược lại góc vuông nội tiếp thì chắn nửa đường tròn.
– Góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.

- Các dạng toán về đường tròn ôn thi vào 10
Dạng 1: Chứng minh hai góc bằng nhau.
Cách chứng minh:
– Chứng minh hai góc cùng bằng góc thứ ba
– Chứng minh hai góc bằng với hai góc bằng nhau khác
– Hai góc bằng tổng hoặc hiệu của hai góc theo thứ tự đôi một bằng nhau
– Hai góc cùng phụ (hoặc cùng bù) với góc thứ ba
– Hai góc cùng nhọn hoặc cùng tù có các cạnh đôi một song song hoặc vuông góc
– Hai góc so le trong, so le ngoài hoặc đồng vị
– Hai góc ở vị trí đối đỉnh
– Hai góc của cùng mộ tam giác cân hoặc đều
– Hai góc tương ứng của hai tam giác bằng nhau hoặc đồng dạng
– Hai góc nội tiếp cùng chắn một cung hoặc chắn hai cung bằng nhau.
Dạng 2: Chứng minh hai đoạn thẳng bằng nhau
Cách chứng minh:
– Chứng minh hai đoạn thẳng cùng bằng đoạn thứ ba
– Hai cạnh của một tam giác cân hoặc tam giác đều
– Hai cạnh tương ứng của hai tam giác bằng nhau
– Hai cạnh đối của hình bình hành (chữ nhật, hình thoi, hình vuông)
– Hai cạnh bên của hình thang cân
– Hai dây trương ứng hai cung bằng nhau trong một đường tròn hoặc hai đường bằng nhau. Tính chất 2 tiếp tuyến cắt nhau
Dạng 3: Chứng minh hai đường thẳng song song
Cách chứng minh:
– Chứng minh hai đường thẳng cùng song song với đường thẳng thứ ba
– Chứng minh hai đường thẳng cùng vuông góc với đường thẳng thứ ba
– Chứng minh chúng cùng tạo với một cát tuyến hai góc bằng nhau: ở vị trí so le trong; ở vị trí so le ngoài; ở vị trí đồng vị.
– Là hai dây chắn giữa chúng hai cung bằng nhau trong một đường tròn
– Chúng là hai cạnh đối của một hình bình hành, chữ nhật, hình vuông, …
Dạng 4: Chứng minh hai đường thẳng vuông góc
Cách chứng minh:
– Chúng cùng song song với hai đường thẳng vuông góc khác.
– Chứng minh chúng là chân đường cao trong một tam giác.
– Đường kính đi qua trung điểm của dây và dây không đi qua tâm.
– Chúng là phân giác của hai góc kề bù nhau.
– Tính chất 2 đường chéo hình thoi, hình vuông










Để lại một bình luận