Dạng bài toán về chứng minh tứ giác nội tiếp
Các dạng bài toán chứng minh tứ giác nội tiếp đường tròn có lời giải được nhiều bạn đọc tìm kiếm. Vì vậy pqt.edu.vn tạo topic tổng hợp các bài tập về chứng minh tứ giác nội tiếp để làm tài liệu tham khảo.
Trước khi bước vào giải các bài tập về tứ giác nội tiếp dưới đây các bạn cần nắm chắc kiến thức lý thuyết mà chúng tôi đã trình bày chi tiết ở bài Dấu hiệu nhận biết tứ giác nội tiếp để trả lời câu hỏi được tốt hơn.
Tại sao là 1001 câu hỏi về CM tứ giác nội tiếp mà không phải con số thực tế của bài viết?
Vì đây là bài viết tổng hợp, sẽ được pqt.edu.vn cập nhật liên tục các câu hỏi mới, sáng tạo. Do đó 1001 là con số tượng trưng cho điều… không có hồi kết.
Qua đây chúng tôi cũng mong muốn được sự đóng góp các dạng bài toán hay về chứng minh tứ giác nội tiếp đường tròn của quý độc giả để tạo nguồn bài tập tham khảo phong phú hơn
1001 Bài toán chứng minh tứ giác nội tiếp đường tròn có đáp án
Bài toán 1.
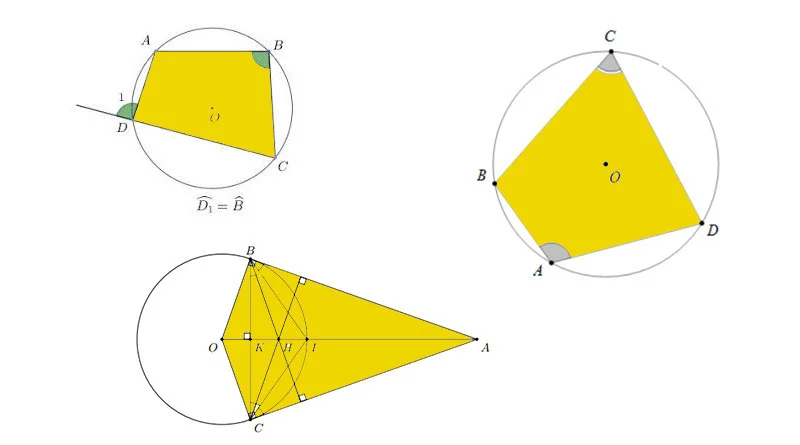
Cho tam giác ABC, có các đường cao AD, BE, CF cắt nhau tại H. Chứng minh các tứ giác AEHF, CDHE, BFHD, AEDB, BFEC, CDFA là các tứ giác nội tiếp.
Gợi ý.
Quan sát hình vẽ, nhận thấy được các tứ giác AEHF, CDHE, BFHD là các tứ giác có cặp góc đối 90 độ nên ta dùng cách 2 trong bài viết Cách chứng minh tứ giác nội tiếp để làm bài.
Quan sát hình vẽ, nhận thấy các hình AEDB, BFEC, CDFA là các tứ giác có hai đỉnh kề cùng nhìn một cạnh dưới một góc vuông nên ta dùng cách 5 để chứng minh tứ giác nội tiếp đường tròn.
Bài toán 2.
Cho tam giác ABC nhọn, vẽ nửa đường tròn tâm O đường kính BC cắt hai cạnh AB, AC lần lượt tại F và E. Gọi H là giao điểm của BE, CF. Chứng minh tứ giác AFHE nội tiếp.
Gợi ý.
Từ hình vẽ, nhận biết tứ giác AFHE có góc AFH = góc AEH = 90 độ. Muốn vậy ta cần chỉ ra BE vuông với C tại E, CF vuông với AB tại F bằng việc sử dụng góc nội tiếp chắn nửa đường tròn, từ đó dùng cách 2 để chứng minh tứ giác nội tếp.
Bài toán 3.
Cho đường tròn (O;R). Từ điểm M nằm ngoài đường tròn (O) vẽ hai tiếp tuyến MA, MB tới đường tròn (A, B là các tiếp điểm). Chứng minh tứ giác MAOB nội tiếp.
Gợi ý.
Từ hình vẽ, nhận biết tứ giác MAOB có góc A bằng góc B bằng 90 độ. Muốn vậy ta cần chỉ ra MA vuông góc với OA tại A và MB vuông góc với OB tại B từ tính chất tiếp tuyến của đường tròn. Từ đó dùng cách 2 để chứng minh tứ giác nội tiếp.
Bài toán 4.
Cho đoạn thẳng AB, điểm A nằm giữa M và B. Vẽ đường tròn (O) đường kính AB. Từ M kẻ đường thẳng d vuông góc với MB tại M, lấy điểm N tùy ý trên d sao cho NA và NB lần lượt cắt (O) tại E và F. Chứng minh các tứ giác MNFA, MNBE nội tiếp.
Gợi ý.
Đã có sẵn góc NMA = 90 độ (do d vuông góc với MB tại M), nên
- Ta cần chỉ ra góc AFN bằng 90 độ từ góc nội tiếp chắn nửa đường tròn, từ đó dùng cách 2 để chứng minh tứ giác MNFA nội tiếp
- Ta cần chỉ ra góc NEB bằng 90 độ từ góc nội tiếp chắn nửa đường tròn, từ đó dùng cách 5 để chứng minh tứ giác MNBE nội tiếp










Để lại một bình luận