Hệ thức lượng trong tam giác vuông (lý thuyết và bài tập)

Lý thuyết hệ thức lượng trong tam giác vuông toán lớp 9

Lý thuyết về hệ thức lượng trong tam giác vuông học ở chương trình lớp 9 phần hình học. Các công thức hệ thức lượng trong tam giác vuông này sẽ áp dụng xuyên suốt chương trình học toán lớp 9, vì vậy pqt.edu.vn sẽ trình bày chi tiết chuyên đề hệ thức lượng áp dụng trong tam giác vuông này để các bạn tiện theo dõi.

Xem thêm:

Chuyên đề Rút Gọn Biểu Thức toán lớp 9

Đề Thi Thử Toán Vào 10 Có Đáp Án Trắc Nghiệm và Tự Luận

Đề cương ôn thi vào 10 môn toán

* Quy ước các cạnh trong tam giác vuông

Cho tam giác vuông ABC có đường cao AH như hình vẽ ta có:

Cạnh huyền là BC
Cạnh góc vuông AB, có hình chiếu lên cạnh huyền là BH
Cạnh góc vuông AC, có hình chiếu lên cạnh huyền là CH
Đường cao là AH.

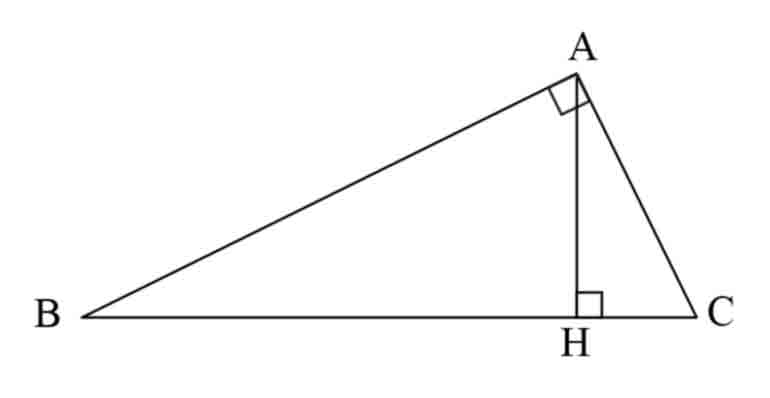
Từ đó ta có 5 định lý hệ thức lượng cần nhớ trong tam giác vuông như sau (lưu ý chỉ được áp dụng trong tam giác vuông):

Sau khi học tốt chuyên đề hệ thức lượng trong tam giác vuông các bạn có thể thử sức mình với bộ đề thi học kì 1 toán 9 có đáp án để củng cố kiến thức toán lớp 9 học kì 1 của mình

1. Hệ thức: Cạnh huyền – cạnh góc vuông (Định lý Pitago)

Định lý Pytago: Trong tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài hai cạnh góc vuông.

Hệ thức: BC² = AB² + AC²

2. Hệ thức: Cạnh góc vuông – cạnh huyền – hình chiếu của cạnh góc vuông

Trong tam giác vuông, bình phương độ dài mỗi cạnh góc vuông bằng tích độ dài cạnh huyền với hình chiếu của cạnh góc vuông đó lên cạnh huyền.

Hệ thức: AB² = BC.BH   và   AC² = BC.CH

3. Hệ thức: Đường cao – hình chiếu của cạnh góc vuông

Trong tam giác vuông, bình phương độ dài đường cao bằng tích độ dài hình chiếu của hai canh góc vuông lên cạnh huyền.

Hệ thức: AH² = BH.CH

4. Hệ thức: Đường cao – cạnh góc vuông

Trong tam giác vuông, nghịch đảo bình phương độ dài đường cao bằng tổng nghịch đảo bình phương độ dài hai cạnh góc vuông.

Hệ thức: 1/AH² = 1/AB² + 1/AC²

5. Hệ thức: Đường cao – cạnh góc vuông – cạnh huyền

Trong tam giác vuông, tích độ dài hai cạnh góc vuông bằng tích độ dài cạnh huyền với đường cao tương ứng.

Hệ thức: AB.AC = BC.AH

Dạng bài tập về hệ thức lượng trong tam giác vuông

Từ 5 định lý nêu trên chúng ta triển khai 6 dạng bài tập về hệ thức lượng trong tam giác vuông dưới đây:

Dạng 1: Dùng hệ thức lượng tính độ dài cạnh, đường cao, hình chiếu trong tam giác vuông

a. Phương pháp.

Đây là những bài toán chúng ta sẽ tính toán trực tiếp trong một tam giác vuông cho trước. Để giải bài toán này ta làm như sau:

– Xác định bài yêu cầu tính: “cạnh góc vuông” hay “đường cao” hay “hình chiếu của cạnh góc vuông”?
– Kiểm tra bài đã cho dữ kiện nào.
– Xác định hệ thức liên hệ giữa cái đã cho và cái cần tính.

b. Bài tập vận dụng

Bài 1. Biết tỉ số các cạnh góc vuông của một tam giác vuông là 5:6 ; cạnh huyền 122cm. Tính độ dài hình chiếu của mỗi cạnh góc vuông lên cạnh huyền.

Bài 2. Biết tỉ số các cạnh góc vuông của một tam giác vuông là 3:7 ; đường cao ứng với cạnh huyền là 12cm. Tính độ dài hình chiếu của mỗi cạnh góc vuông lên cạnh huyền.

Bài 3. Cho ∆ABC vuông tại A, kẻ đường cao AH. Biết AB = 4cm, AC = 7,5cm. Tính HB, HC.

Bài 4. Cho ∆ABC vuông tại A, kẻ đường cao AH. Biết AB = 15cm, HC = 16cm. Tính BC, AC, AH.

Bài 5. Cho ∆ABC vuông tại A, kẻ đường cao AH. Biết AH = 12cm, BC = 25cm. Tính AB, AC.

Bài 6. Cho ∆ABC vuông tại A, kẻ đường cao AH. Biết AB = 6cm, BH = 3cm. Tính AH, AC, CH.

Bài 7. Cho ∆ABC vuông tại A, đường cao AH. Tính diện tích ∆ABC biết AH = 12cm, BH = 9cm.

Bài 8. Cho tam giác vuông, biết tỉ số giữa các cạnh góc vuông là 5/12, cạnh huyền là 26. Tính độ dài các cạnh góc vuông và hình chiếu các cạnh góc vuông trên cạnh huyền.

Bài 9. Cho ∆ABC vuông tại A. Biết AB/AC = 5/7 . Đường cao AH = 15cm. Tính HB, HC.

Bài 10. Cho ∆ABC vuông tại A. Kẻ đường cao AH, tính chu vi ∆ABC biết AH = 14cm, HB/HC = 1/4.

Dạng 2: Tam giác vuông liên quan các đường: phân giác, trung tuyến, trung trực

a. Phương pháp.

Trong tam giác vuông, các hệ thức của tam giác vuông vẫn được áp dụng.

Chú ý:

+ Đường phân giác => Tỉ lệ đoạn thẳng theo tính chất đường phân giác

+ Đường trung tuyến liên quan tới trung điểm

+ Đường trung trực thì liên quan tới vuông góc tại trung điểm.

b. Bài tập vận dụng

Bài 1. Cho ∆ABC vuông tại A, AB = 12cm, AC = 16cm, phân giác AD, đường cao AH. Tính HD, HB, HC.

Bài 2. Cho ∆ABC vuông tại A, phân giác AD, BD/BC = 3/7 , BC = 20. Tính AB, AC.

Bài 3. Cho ∆ABC vuông tại A, phân giác AD, gọi E, F lần lượt là hình chiếu của D lên AB và AC. Biết BD=3, DC=4. Chứng minh ADEF là hình vuông, tính diện tích của nó?

Bài 4. Cho tam giác ABC vuông tại A, AB = 24, AC = 32. Đường trung trực BC cắt AC, BC theo thứ tự tại D và E. Tính DE?

Bài 5. Trong một tam giác vuông tỉ số giữa đường cao và đường trung tuyến xuất phát từ đỉnh góc vuông là 40:41. Tính tỉ số độ dài các cạnh góc vuông của tam giác vuông đó?

Bài 6. Trong một tam giác vuông, phân giác của góc nhọn chia cạnh đối diện thành hai phần tỉ lệ với 4:5 và 3:5. Biết chu vi tam giác bằng 72. Tính các cạnh của tam giác đó?

Bài 7. Trong một tam giác vuông, phân giác của góc vuông chia cạnh huyền thành hai phần có độ dài 1cm và 3cm. Hỏi đường cao tương ứng với cạnh huyền chia cạnh huyền theo tỉ số nào?

Dạng 3: Nhận biết tam giác vuông rồi dùng hệ thức lượng để tính

a. Phương pháp.

– Tính bình phương các cạnh của tam giác, nếu tổng bình phương hai cạnh bằng bình phương cạnh còn lại => tam giác đó vuông.

– Áp dụng các hệ thức của tam giác vuông để tính.

b. Bài tập vận dụng.

Bài 1. Cho ∆ABC biết BC = 7.5cm, AC = 4.5cm, AB = 6cm.

a) ∆ABC là tam giác gì? Tính đường cao AH của ∆ABC.
b) Tính độ dài các cạnh BH

Bài 2. Cho ∆ABC biết BC = 50cm, AC = 14cm, AB = 48cm. Tính độ dài phân giác góc C?

Dạng 4: Kết hợp tỉ số đồng dạng và hệ thức lượng trong tam giác vuông để tìm dộ dài

a. Phương pháp.

• Có thể gọi ẩn độ dài các đoạn thẳng cần tính.
• Từ tam giác đồng dạng => Tỉ số độ dài => liên hệ giữa các ẩn độ dài (1)
• Từ hệ thức lượng => Liên hệ giữa các ẩn độ dài (2)
• Từ (1) và (2), giải hệ tìm ra các ẩn độ dài.

b. Bài tập vận dụng.

Bài 1: Cho tam giác ABC vuông tại A, BC = 5căn2 cm. Hình vuông ADEF cạnh 2cm có D thuộc AB, E thuộc BC, F thuộc AC. Tính các độ dài AC, AB.

Bài 2: Cho tam giác ABC cân tại A, đường cao ứng với cạnh đáy có độ dài 15,6cm, đường cao ứng với cạnh bên dài 12cm. Tính độ dài cạnh đáy BC.

Dạng 5: Kẻ đường phụ để tạo yếu tố đặc biệt có liên quan hệ thức lượng tam giác vuông

a. Phương pháp.

– Yếu tố đặc biệt thường gặp khi kẻ thêm hình:

+ Tam giác cân (đều) có chứa cạnh cần tính.

+ Tam giác vuông có chứa cạnh đã biết và cạnh cần tính.

b. Bài tập vận dụng.

Bài 1: Tam giác ABC vuông tại A, gọi I là giao điểm của các đường phân giác. Biết AB = 5cm, IC = 6cm. Tính độ dài BC.

Bài 2: Tam giác ABC vuông tại A, gọi I là giao điểm của các đường phân giác. Biết IB = căn5 cm, IC = căn 10 cm. Tính các độ dài AB, AC.

Bài 3: Tam giác ABC cân tại A, gọi I là giao điểm của các đường phân giác của góc A và góc B. Biết IA = 2căn5 cm, IB = 3cm. Tính độ dài AB.

Dạng 6: Các bài toán về tứ giác có dùng hệ thức lượng trong tam giác vuông

Bài 1. Cho hình chữ nhật ABCD, qua A kẻ đường vuông góc với BD tại H. Biết AB = 20, AH = 12. Tính chu vi hình chữ nhật.

Bài 2. Cho hình vuông ABCD, AB = 15cm, áp dụng các đường chéo AC  và BD vuông góc với nhau tại O, tính:

a) OB, OD, AC
b) Diện tích hình vuông

Bài 3. Cho hình thang ABCD vuông tại A và D. Biết AB = 45cm, cạnh đáy CD = 10cm, BC = 37cm. Tính chiều cao và diện tích hình thang.

Bài 4. Cho hình thang ABCD có chu vi là 52cm, đáy nhỏ AB bằng cạnh bên AD và BC, đáy lớn DC = 22cm. Tính chiều cao hình thang.

Bài 5. Cho tứ giác ABCD có hai đường chéo vuông góc với nhau.

Chứng minh: AD² + BC² = AB² + CD²

Qua hai phần lý thuyết và các dạng toán về hệ thức lượng trong tam giác vuông ở trên hi vọng giúp ích được cho các bạn trong việc học toán lớp 9. Chúng tôi sẽ sớm hoàn thiện bộ bài tập luyện tập cho chuyên đề hệ thức lượng trong tam giác vuông này và bổ sung vào bài viết để gửi đến quý đọc giả trong thời gian sớm.

Click Download file word chuyên đề hệ thức lượng trong tam giác vuông.

Lưu ý để học tốt phần hệ thức lượng trong tam giác vuông

Để học tốt kiến thức hệ thức lượng trong tam giác vuông thì trước tiên các em cần lần lượt nắm rõ các bước cơ bản dưới đây:

• Xác định được quy ước về cạnh trong tam giác vuông (xem lại phần đầu bài viết)
• Nắm rõ công thức về 5 hệ thức lượng tam giác vuông, xem lại TẠI ĐÂY
• Làm thành thạo các bài tập trong sgk và sách bài tập.
• Nâng cao kiến thức bằng cách rèn luyện bài tập ở Chuyên đề ôn thi vào 10 môn toán

Ngoài ra: Tinh thần tự học rất quan trọng, hãy “thật sự” tự giác và tập trung tinh thần trong thời gian học bài ở trường cũng như ở nhà. Sau đó là hỏi bạn, hỏi thầy cô những gì còn chưa hiểu để kịp thời củng cố kiến thức.

Câu hỏi thường gặp