Cách chứng minh tứ giác nội tiếp đường tròn đạt điểm tối đa

Lý thuyết về tứ giác nội tiếp đường tròn

Chứng minh tứ giác nội tiếp đường tròn toán lớp 9 là vấn đề quan tâm của nhiều học sinh, vì vậy PQT.EDU.VN sẽ trình bày cụ thể, chi tiết nhất về chuyên đề cách chứng minh tứ giác nội tiếp đường tròn hay còn gọi là đường tròn ngoại tiếp tam giác, nhằm giúp các bạn làm bài thi đạt điểm tối đa câu hỏi về tứ giác nội tiếp này.

Trước khi đi vào cụ thể cách chứng minh tứ giác nội tiếp thì các bạn cần nắm kiến thức lý thuyết về tứ giác nội tiếp đường tròn dưới đây:

Sau đó hãy rèn luyện với 1001 Dạng bài toán chứng minh tứ giác nội tiếp đường tròn

Định nghĩa tứ giác nội tiếp đường tròn:

Một tứ giác có bốn đỉnh cùng nằm trên một đường tròn gọi là tứ giác nội tiếp đường tròn.

Lưu ý khi chứng minh tứ giác nội tiếp đường tròn

Để làm tốt các bài tập chứng minh tứ giác nội tiếp đường tròn, các bạn cần đặc biệt lưu ý các vấn đề sau:

• Đề bài yêu cầu chứng minh đường tròn (O;R) ngoại tiếp tứ giác ABCD cũng đồng nghĩa với việc chứng minh tứ giác ABCD nội tiếp đường tròn (O;R).
• Cần đọc kỹ đề bài và vẽ hình, đánh dấu các đỉnh chính xác theo giả thiết bài toán.
• Tận dụng các giả thiết đã cho để chọn phương pháp chứng minh phù hợp.
• Dùng các cách chứng minh được trình bày dưới đây để hoàn thành bài tập.

Cách chứng minh tứ giác nội tiếp đường tròn

Có nhiều phương pháp chứng minh tứ giác nội tiếp, ở bài viết này chúng tôi sẽ trình bày theo thứ tự các cách được sử dụng phổ biến bởi tính nhanh, gọn, rõ ràng của chúng. Các cách này được sử dụng dựa trên Dấu hiệu nhận biết tứ giác nội tiếp

Cách 1. Sử dụng định nghĩa tứ giác nội tiếp đường tròn.

Ta dựa vào định nghĩa “Một tứ giác có bốn đỉnh cùng nằm trên một đường tròn gọi là tứ giác nội tiếp đường tròn.” để làm bài, cụ thể:

Chứng minh các đỉnh của tứ giác cùng cách đều một điểm I một khoảng cách bằng R thì tứ giác sẽ nội tiếp đường tròn tâm I bán kính R.

Cách 2. Sử dụng định lý đảo của tứ giác nội tiếp

Căn cứ vào định lý đảo “Nếu một tứ giác có tổng số đo hai góc đối diện bằng 180 độ thì tứ giác đó nội tiếp được đường tròn.” để làm bài, cụ thể:

Chứng minh tứ giác có tổng hai góc đối bằng 180 độ.

Ví dụ: Để chứng minh tứ giác ABCD nội tiếp đường tròn ta cần chỉ ra góc A + C = 180 độ hoặc góc B + D = 180 độ

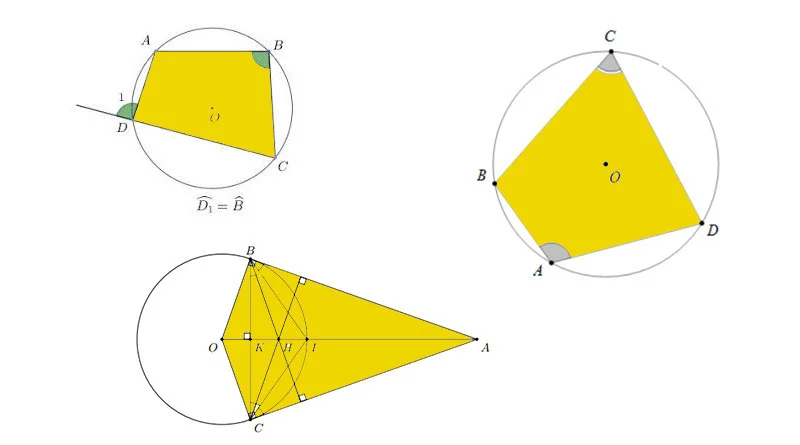
Cách 3. Chứng minh tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó

Phương pháp này được phát triển từ cách thứ 2 ở trên theo giải thích dưới đây

Hai phương pháp tiếp theo đây đều sử dụng chung hệ quả của tứ giác nội tiếp.

Cụ thể ta chứng minh hai đỉnh kề nhau của tứ giác cùng nhìn một cạnh dưới hai góc bằng nhau. Với 2 trường hợp ứng với 2 cách 4 và 5:

Cách 4. Tứ giác có hai góc đối nhau cùng là góc vuông thì tứ giác đó nội tiếp đường tròn.

Cách 5. Tứ giác có hai đỉnh cùng nhìn một cạnh dưới một góc vuông thì nội tiếp đường tròn.

Cách 6. Tứ giác có tổng số đo hai cặp góc đối bằng nhau thì tứ giác đó nội tiếp đường tròn

Ví dụ: Cho một tứ giác tứ giác ABCD. Để ABCD là tứ giác nội tiếp đường tròn ⇔ góc A + góc C = góc B + góc D.

Cách 7. Chỉ ra tứ giác thuộc trường hợp tứ giác đặc biệt

Tứ giác là các hình sau đây sẽ nội tiếp đường tròn:
– Hình vuông
– Hình chữ nhật
– Hình thoi
– Hình bình hành
– Hình thang cân

Để chứng minh được tứ giác thuộc một trong bốn hình đặc biệt nêu trên, các bạn cần nắm tính chất của các hình đó được trình bày chi tiết các bài viết

Dấu hiệu nhận biết hình thoi

Dấu hiệu nhận biết hình bình hành

Dấu hiệu nhận biết hình vuông

Dấu hiệu nhận biết hình chữ nhật